Quantum Algorithm (2) - 양자 알고리즘의 특성 및 계산 복잡도(Complexity Classes NP & P)
"양자 컴퓨터가 현재의 슈퍼컴퓨터보다 수백만 배 빠르다"는 이야기를 들어보셨나요? 이런 주장들이 과연 사실일까요? 오늘은 양자 컴퓨터가 전통적인 컴퓨터보다 정말로 더 빠른지, 그리고 어떤 문제에서 더 빠른지에 대해 알아보겠습니다.
전통적인 컴퓨터는 비트(bit)를 사용합니다. 비트는 0 또는 1, 둘 중 하나의 값만 가질 수 있죠. 하지만 양자 컴퓨터의 큐비트(qubit)는 다릅니다.
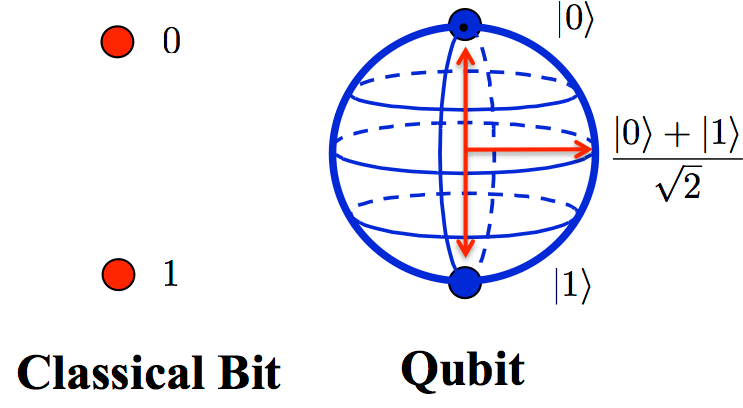
클래식 비트: 0 또는 1
양자 큐비트: α|0⟩ + β|1⟩ (α와 β는 복소수)
n개의 큐비트는 차원의 복소수 벡터로 표현됩니다. 예를 들어:
- 10 큐비트 = 1,024차원
- 20 큐비트 = 1,048,576차원
- 50 큐비트 = 1,125,899,906,842,624차원
큐비트(qubit)이 증가할 때 마다 지수적으로 차원이 늘어나는 것이 비트(bit)에 비해 가지는 장점입니다.
많은 사람들이 오해하는 부분이 있습니다. "양자 컴퓨터는 모든 가능성을 동시에 계산할 수 있으니까 무조건 빠르다"고 생각하는 것이죠. 하지만 현실은 조금 다릅니다. "양자 알고리즘은 모든 가능한 입력을 동시에 처리하는 양자 병렬성 덕분에 기존 알고리즘보다 훨씬 빠르다" 또한 반쪽짜리 설명입니다.
사실 같은 말임
양자 컴퓨터는 중간 과정에서는 복소수 계산을 할 수 있지만, 측정 시에는 0과 1의 이진 값만 얻을 수 있습니다. 이는 마치 수많은 평행우주에서 동시에 계산을 한 후, 그 중 하나의 결과만 볼 수 있는 것과 같습니다.

따라서 양자 시스템에서 측정을 하면 결과적으로 하나의 답만 얻게 되며, 대부분의 경우 틀린 답이 나올 확률이 맞는 답이 나올 확률보다 훨씬 높습니다. 그렇다면 양자 알고리즘의 진정한 힘은 어디서 나오는 걸까요?

양자 알고리즘의 핵심은 단순한 중첩 상태 활용이 아니라, 이러한 중첩 상태들을 교묘하게 조작하여 측정 시 올바른 답이 나올 확률을 극대화하는 것입니다. 이는 고전적 관점에서는 볼 수 없는 수학적 패턴을 양자적 관점에서 활용하는 것이며, 단순한 속도 향상이 아닌 완전히 새로운 접근법을 의미합니다.
알고리즘의 효율성을 논하기 전에, 먼저 문제의 복잡도를 어떻게 측정하는지 이해해야 합니다. 다음과 같은 인수분해 문제들을 생각해보겠습니다:
- 35를 두 개의 1보다 큰 정수의 곱으로 나타내기
- 187을 두 개의 1보다 큰 정수의 곱으로 나타내기
- 2,407을 두 개의 1보다 큰 정수의 곱으로 나타내기
- 88,631을 두 개의 1보다 큰 정수의 곱으로 나타내기
첫 번째 문제는 쉽게 풀 수 있지만, 숫자가 커질수록 문제는 급격히 어려워집니다. 반면, 다음과 같은 검증 문제들을 생각해보겠습니다:
- 7 × 5 = 35인지 확인하기
- 11 × 17 = 187인지 확인하기
- 29 × 83 = 2,407인지 확인하기
- 337 × 263 = 88,631인지 확인하기
이러한 검증 문제들은 상대적으로 쉽게 해결할 수 있습니다.
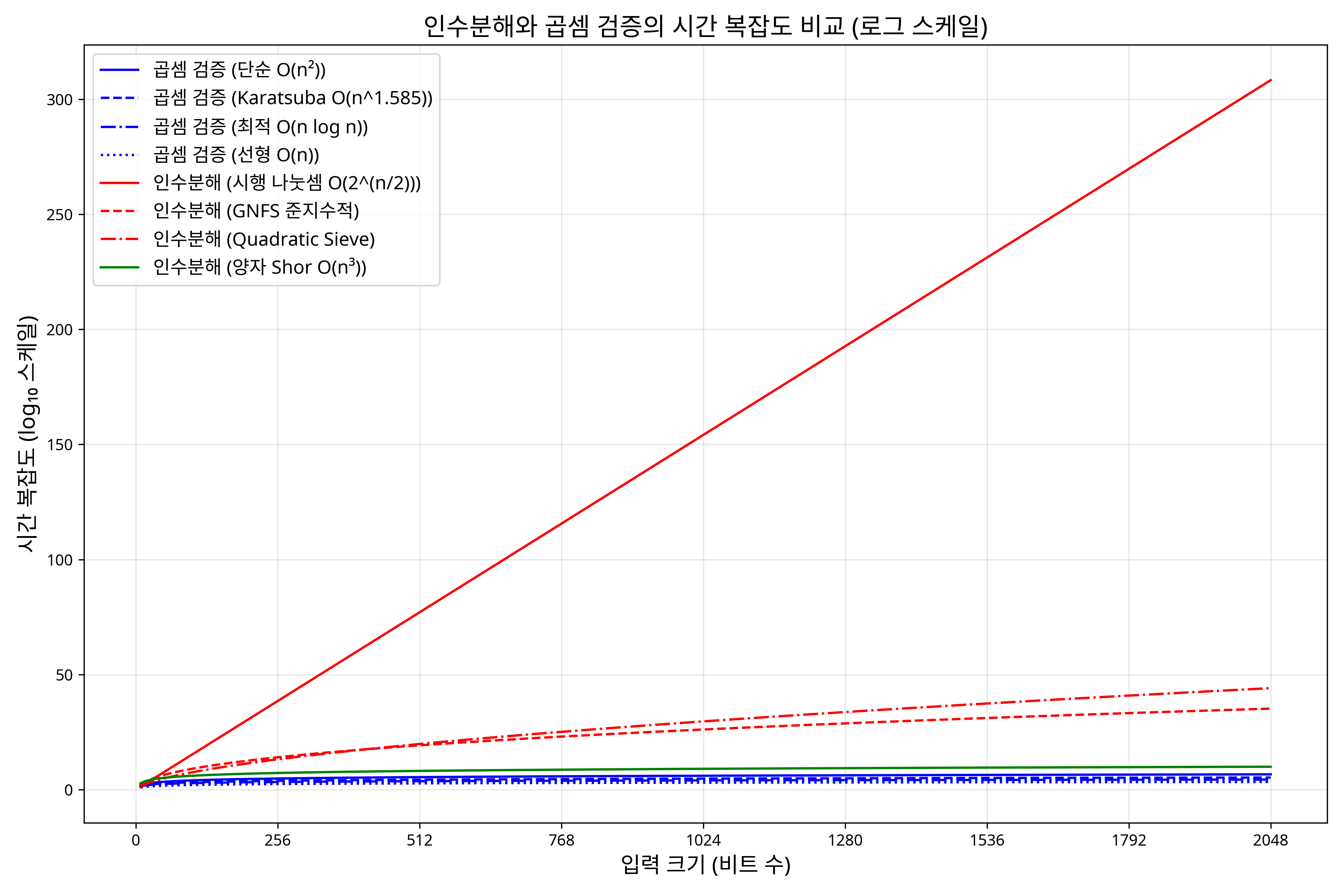
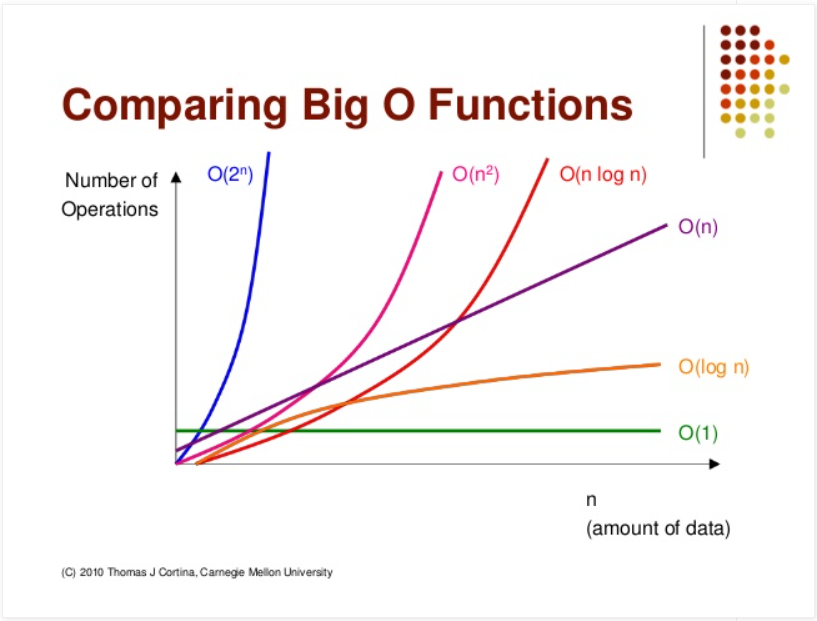
입력 크기를 n이라 할 때, 문제 해결에 필요한 시간을 T(n)이라고 합니다. 복잡도 이론에서는 n이 커짐에 따라 T(n)이 얼마나 커지는지에 따라 문제를 분류합니다:
다항식 시간 (Polynomial Time): 양의 상수 k와 p에 대해 가 성립하는 경우
지수 시간 (Exponential Time): 양의 상수 k와 c > 1에 대해 이 성립하는 경우
다항식 시간으로 해결 가능한 문제는 다루기 쉬운(tractable) 문제로, 지수 시간이 필요한 문제는 다루기 어려운(intractable) 문제로 분류됩니다. 이는 아무리 컴퓨터 성능이 향상되어도 지수 시간 문제는 입력 크기가 조금만 증가하면 현실적으로 해결 불가능해지기 때문입니다.
P 클래스 (Polynomial time): 다항식 시간 내에 해결할 수 있는 결정 문제들의 집합
예시:
- 두 n×n 행렬의 곱셈
- 그래프에서 최단 경로 찾기
- 주어진 수가 소수인지 판별하기
NP 클래스 (Nondeterministic Polynomial time): 다항식 시간 내에 검증할 수 있는 결정 문제들의 집합 (=답이 뭔지 모를 때는 시간이 오래 걸리지만 답이 true이고 그 답이 주어졌을 때 그게 맞다는 것은 다항 시간안에 금방 체크할 수 있는 문제들의 집합) (=푸는 법은 몰라도 채점은 빠르게 할 수 있다.)
예시:
- 불 만족가능성 문제 (SAT): 주어진 불린 공식이 참이 될 수 있는지
- 정수 인수분해: 주어진 수의 소인수 찾기
- 해밀턴 경로 문제: 그래프에서 모든 정점을 한 번씩 방문하는 경로 존재 여부
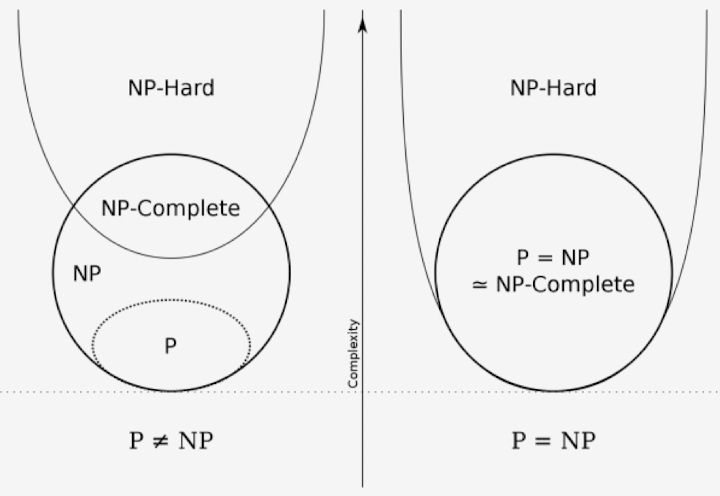
정의상 P ⊆ NP는 자명합니다. 문제를 다항식 시간에 풀 수 있다면, 그 답을 다항식 시간에 검증할 수도 있기 때문입니다. 하지만 그 역이 성립하는지, 즉 P = NP인지는 컴퓨터 과학의 가장 중요한 미해결 문제 중 하나입니다.
1991년 RSA 연구소는 큰 합성수들의 인수분해 챌린지를 발표했습니다. 100자리 수는 비교적 빨리 인수분해되었지만, 300자리 이상의 수들은 여전히 인수분해되지 않았습니다. 이는 인수분해 문제가 실제로는 지수 시간이 필요할 가능성을 시사합니다.
2000년 클레이 수학 연구소는 P vs NP 문제를 밀레니엄 문제 중 하나로 선정하여 100만 달러의 상금을 걸었습니다. 이 문제의 해결은 암호학, 최적화, 인공지능 등 다양한 분야에 혁명적 변화를 가져올 것입니다.
대부분의 양자 컴퓨터 과학자들은 P ≠ NP라고 믿습니다. 동시에 양자 컴퓨터가 다항식 시간에 해결할 수 있지만 고전 컴퓨터로는 불가능한 NP 문제들이 존재한다고 생각합니다.
하지만 이를 엄밀하게 증명하는 것은 매우 어려운 일입니다. P ≠ NP를 먼저 증명해야 하는데, 이는 아직 해결되지 않은 문제이기 때문입니다.
이러한 어려움을 해결하기 위해 두 가지 접근법이 사용됩니다:
1. 이론적 접근법: 새로운 복잡도 측정 방법을 개발하여 증명을 더 쉽게 만드는 것
2. 실용적 접근법: 중요한 실세계 문제에 대해 양자 알고리즘을 개발하여 다항식 시간 해결을 보이는 것 (고전적으로는 불가능하다고 믿어지는 문제들)
피터 쇼어(Peter Shor)가 1994년에 개발한 쇼어 알고리즘은 실용적 접근법의 완벽한 예시입니다. 이 알고리즘은:
- 큰 정수의 소인수분해를 다항식 시간에 수행
- 고전 컴퓨터로는 지수 시간이 필요하다고 믿어지는 문제
- 현재 인터넷 보안의 기반인 RSA 암호화에 직접적 위협
쇼어 알고리즘의 시간 복잡도는 으로, n비트 정수에 대해 다항식 시간입니다. 반면 가장 효율적인 고전 알고리즘의 시간 복잡도는 으로 지수 시간입니다.

양자 알고리즘 분석에서 자주 사용되는 개념이 **질의 복잡도(Query Complexity)**입니다. 이는 함수를 평가하는 횟수, 즉 "블랙박스"나 "오라클"에 질의하는 횟수를 세는 방법입니다. (과정은 모르지만 어떤 질문(질의)에 대한 답은 알고있는 무언가(양자시스템에서는 양자 게이트)가 있다고 가정)

이 접근법의 장점은:
- 함수 구현의 세부사항을 고려할 필요가 없음
- 알고리즘의 본질적 효율성에 집중 가능
- 양자 알고리즘과 고전 알고리즘의 비교가 더 명확함
1. 도이치-요자 알고리즘 (Deutsch-Jozsa Algorithm, 1992)
- 문제: 주어진 함수가 상수함수(constant)인지 균형함수(balanced)인지 판별
- 고전: 최악의 경우 번의 질의 필요
- 양자: 단 1번의 질의로 해결
2. 그로버 알고리즘 (Grover's Algorithm, 1996)
- 문제: 정렬되지 않은 데이터베이스에서 특정 항목 검색
- 고전: Ω(n)번의 질의 필요
- 양자: 번의 질의로 해결 가능
3. 쇼어 알고리즘 (Shor's Algorithm, 1994)
- 문제: n비트 정수의 소인수분해
- 고전: (지수 시간)
- 양자: (다항식 시간)
다음 시간에는 도이치-요자 알고리즘 (Deutsch-Jozsa Algorithm)의 토대가 되는 도이치 알고리즘(Deutsch Algorithm)에 대해 알아보겠습니다.